Impulsive Math Geek Gaining Momentum

Earlier this week I heard a loud noise in the morning before getting out of bed. It sounded as though the cats had knocked something over, but it didn't seem too terribly serious, so I didn't trouble about it. I got up at my leisure and went about business as usual. Later that afternoon, however, as I was walking through the entryway, I was startled to see the little shoe rack that sits at the foot of the stairs. It looked like this:

Now, I don't know how you might have responded to seeing your furniture in this condition, but my immediate reaction was to begin pondering just how hard the cat must have hit that surface, and what exactly is the strength of an average sheet of cheap particle board? That's the most natural and obvious question for any math geek, isn't it?

Well, so. Let's play with some numbers. I'll use Kibo as a likely candidate, simply because I know that at his last vet visit he weighed in at 10 pounds. We'll convert that to kilograms for mass, to make things easy; this puts him at about 4.5 kg. The stair from which he likely would have jumped is just over 4 feet, or 1.3 meters, above the shoe rack.
So. That sets up our first question: How much force is generated on impact by a 4.5 kg cat descending from a height of 1.3 meters?
Now, we know from Newton's second law that force equals mass times acceleration.
When an object is in free-fall, neglecting air resistance, the only force operating on that object is the force of gravity. We know that acceleration due to gravity is a constant, with a value of approximately 9.81 m/s2. We'll call that g. This force of gravity acting on an object is what we refer to as the weight of the object. This gives us the formula for determining weight:
We can calculate Kibo's weight, then, as
So here's the thing: the mass of the cat is a constant. The acceleration due to gravity is a constant. Therefore the force of gravity acting on that mass must also be a constant, independent of velocity or distance travelled — and we know that's true, because that's what we call weight and we know the cat's weight doesn't change. So where do we take into account the height from which the cat jumped? If that were all there were to it, the cat would exert the same force while standing on the surface of the shelf as it would by leaping down from a height of 4 feet, or even 20. And that can't be right. I puzzled over this for quite a while, working equations this way and that, and concluded that there must be forces at work here beyond my reckoning!
Momentum
I then turned my attention to the concept of momentum. Momentum is a vector quantity, which can be thought of as a measure of the difficulty of bringing an object to rest. (That sounds promising!) The momentum of a particle is defined as the product of its mass and velocity:
Okay, now we're getting somewhere. We can find out how fast the cat was traveling at the time of impact using the constant acceleration formula, since we know that acceleration due to gravity is constant. With constant acceleration, the velocity at any given time is equal to the initial velocity (v0) plus the product of time and acceleration:
You can reason that out like this: Suppose you start with a velocity of zero, and you accelerate at 5 meters per second per second. After 1 second, you'd be traveling at a velocity of 5 m/s, and after 2 seconds, you'd be traveling at a velocity of 10 m/s, etc.
Okay, that's good, but I don't know how long it took the cat to reach the ground. Since the velocity of an object is the change in position with respect to time, the constant acceleration formula shown above can be reworked to express velocity as a function of the distance travelled. (I'm sure glad I kept my college physics textbook!) Skipping the messy math, this comes out to the following:
Since we know the distance traveled, let's put in some numbers. The initial velocity is zero, acceleration is 9.81 m/s2, and Δx is 1.3 meters, so...
v2 = 25.506 m2/s2
v ≈ 5.05 m/s
...the cat was travelling about 5.05 meters per second when it hit the shoe rack. Now we can use that to calculate momentum:
p = (4.5 kg)(5.05 m/s)
p = 22.725 kg⋅m/s
Alright, this is good, but we still haven't discovered how this relates to the force with which the cat hit the shelf. To do that, we need to talk about impulse.
Impulse
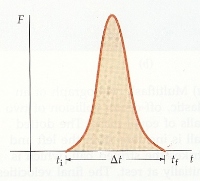
When two objects collide, they interact for a very short time with a large amount of force. (How much force is exactly the thing we want to know!) The graph on the right illustrates the amount of force exerted by one object on another during a collision. The area under the F-versus-t curve is the total force exerted during the time of impact. This is referred to as impulse. And the impulse, conveniently, happens to be equal to the change in momentum:
As with momentum, units of impulse are newton-seconds, or kilogram-meters per second.
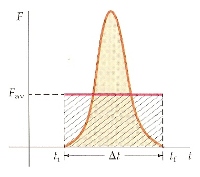
One more step, and we're almost there: the average force exerted over the interval Δt, as shown in the figure to the left, is defined as
| Fav | = | I Δt |
= | Δp Δt |
The average force Fav for this time interval is the constant force that gives the same impulse as the actual force during that interval. The shaded rectangular area FavΔt is the same as the area under the F-versus-t curve. Calculating this average force will tell us how hard the cat hit the shoe rack!
Alright, so, we need to know both Δp and Δt. Now, if the cat landed on the shoe rack and stopped there, we would know that the final momentum was zero. Given the fact that the top shelf is (or was) about a foot high, we can guess that the cat most probably hit the shelf and jumped off. If I wanted to be really super accurate, I would need to estimate the velocity of the cat as it left the shoe rack. But to keep things simple (I think it's been complicated enough so far, personally), we will just assume that the final momentum was zero. This will inflate our results slightly.
Assuming then, that the final momentum was zero, we know that Δp is equal to the momentum that the cat had at the moment of impact, which as we calculated above, is 22.725 kg⋅m/s. The time interval can be computed by dividing the distance travelled by the average velocity. Distance travelled during the time of impact? What is that? Well, let's look at the shelf again:

I measured the distance from the lower shelf to the top shelf at the left corner, which I will take to be the starting position. I then measured from the lower shelf to the bottom of the broken section, taking that to be the end position. The difference was about 8 centimeters. Since we're assuming that the final velocity is zero, the average velocity will be one half of the starting velocity. Our starting velocity, which we calculated earlier, was 5.05 meters per second, so the average velocity is 2.525 m/s. Now let's calculate the time interval:
| Δt | = | Δy vav |
= | 0.08 m 2.525 m/s |
≈ | 0.0317 s |
Now, finally, we can determine the force of impact:
| Fav | = | Δp Δt |
= | 22.725 kg⋅m/s 0.0317 s |
≈ | 716.88 N |
Comparing that with the cat's weight of 44.15 N, we can see that good ol' Kibo would have come down on that poor shelf with a force approximately 16 times his own weight! That would be like 160 pounds! Supposing he initially landed on his front two paws, which measure about 1 square inch each, that results in a stress of 80 pounds per square inch on a little sheet of cheap particle board that I purchased at Target.
About the Board
Now, you can plainly see by the photo that this material was not capable of withstanding that kind of stress. You would also think that it wouldn't be that difficult to find out the strength of an average piece of particle board. Unfortunately, this task proved more difficult than all the math I've done so far!
I couldn't find exactly what I was looking for on the internet, so I started reading up on things like solid mechanics, stress, tensile strength and all that. Then I noticed this sidebar in my physics textbook, pictured to the right. Apparently just knowing the tensile or compressive strength is not enough! I found an article on Bending on Wikipedia. With tensile stress, you have equal and opposite forces stretching the object. With compressive stress, you have opposite forces pressing in on an object. But with bending, the object experiences compressive stress on the surface that receives the impact, and tensile stress on the opposite side. The rest of this article was way beyond me. You would think that there are enough builders and ordinary folk in the world who just want to know how much weight, or stress, a shelf can support, without needing an advanced engineering degree!
And here is where I will leave it for now. If you find some specification that tells how many pounds per square inch a piece of particle board can support before it breaks, post a comment and let me know. Of I find something later, I'll write another post. (I'm not getting rid of the shoe rack yet, just in case I wind up needing to measure the density of the board!!!)
Comments

Hello Carolyn,
I'm not sure if this is exactly the information you're looking for, as I'm not certain whether the particle board in your shoe rack is this exact type. However it does list the tensile strength of Particle Board of this particular type.
Check section 3, item h.
http://www.resarch.com/viroc/VirocArSpecs.pdf
:)
Argument from Consciousness



